Please see below for a short summary of some recent projects and research directions we are interested in. Our research is kindly funded by NSF award DMS 2111322 (2306064) and 2410140.
Linearized optimal transport (LOT)
We developed a mathematical theory as well as an algorithm which combine linearizations and computational optimal transport to classify potentially high-dimensional data sets consisting of entire point clouds or distributions. This type of data set appears in a large variety of fields, including cancer research, survey analysis, and image and text processing. Within our framework, off-the-shelf machine learning algorithms, which usually only focus on classifying data sets in vector spaces, can be applied, leading to a significant computational improvement. Our method works particularly well for data sets that have been created through elementary transformations like scalings, translations and shearings (see an example from image classification below).
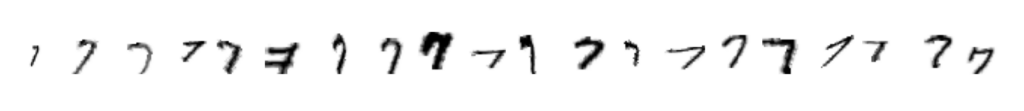
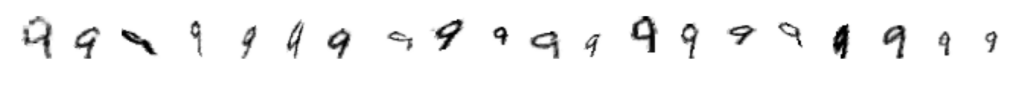
- Caroline Moosmueller, Alex Cloninger. “Linear optimal transport embedding: provable Wasserstein classification for certain rigid transformations and perturbations“, Information and Inference: A Journal of the IMA, Volume 12, Issue 1, pp. 363–389, 2023. DOI
- Varun Khurana, Harish Kannan, Alex Cloninger and Caroline Moosmueller. “Supervised learning of sheared distributions using linearized optimal transport“, Sampling Theory, Signal Processing, and Data Analysis, Volume 21, Article number 1, 2023. DOI (open access)
- Python code
Dimensionality reduction in the Wasserstein space
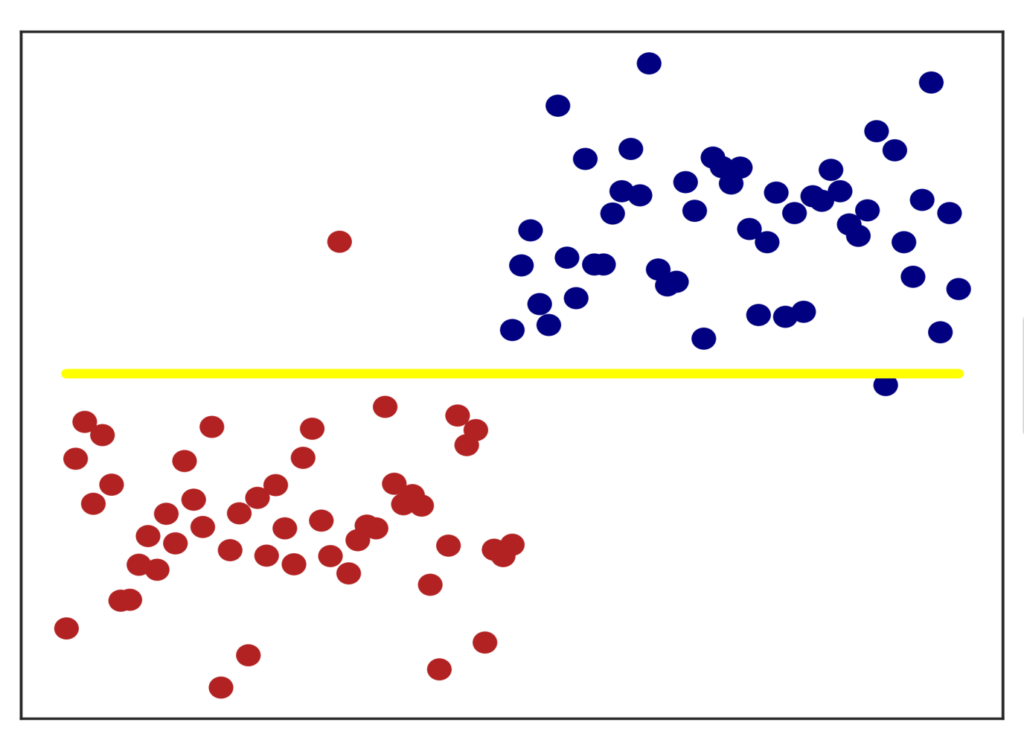
Even when data sets are high-dimensional, they can often be described by a low-dimensional structure or by a small amount of parameters. We present a method to uncover such structures for data sets consisting of point clouds or distributions (see the figure below for a basic example). Most algorithms that uncover low-dimensional structures in data sets require pairwise comparisons between data points, which can be computationally infeasible for large data sets. Our method avoids such computations altogether, making it efficient for large data sets in high dimensions. To this end, we leverage approximation schemes such as LOT and Sinkhorn distances.

- Alex Cloninger, Keaton Hamm, Varun Khurana, Caroline Moosmueller. “Linearized Wasserstein dimensionality reduction with approximation guarantees“, arXiv preprint, 2023.
- Python code