Research

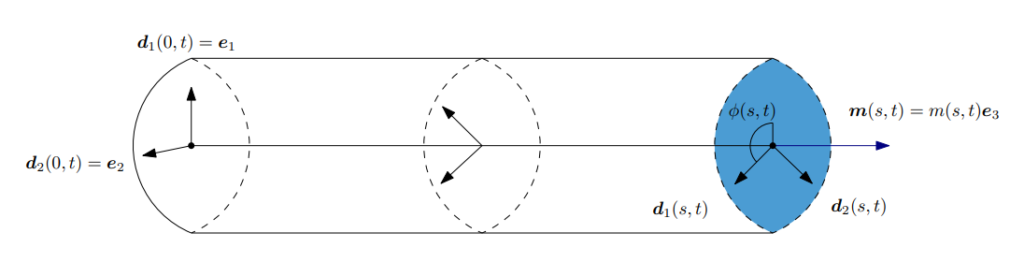
My research is primarily in the study of continuum mechanics, mathematical physics and partial differential equations. In particular, I study theoretical and mathematical aspects of continuum mechanics, concentrating on non-classical models including Cosserat rods and gradient continua. The models I’ve worked on go beyond traditional theories of elastic and viscoelastic Cauchy continua, offering the potential to describe complex phenomena—such as fracture or the combined stretching, bending, and twisting of thin rods—in a simple and geometric manner. Moreover, they lead to the creation of new and intriguing partial differential equations.

Publications

1. The conclusion that metamaterials could have negative mass is a consequence of improper constitutive characterisation (with D. Cichra, V. Průša, K. R. Rajagopal, and M. Vejvoda)
   Preprint, 2024, 12 pages. (Submitted)
2. Piecewise linear constitutive relations for stretch-limited elastic strings (with R. Bustamante and K. R. Rajagopal)
   Preprint, 2024, 13 pages. (Submitted)
3. A mathematical justification for nonlinear constitutive relations between stress and linearized strain (with K. R. Rajagopal)
   Z. Angew. Math. Phys. 75 (2024), 17 pp. 
4. Elastic solids with strain-gradient elastic boundary surfaces
   J. Elast., 156 (2024), p. 769-797.
5. A midsurface elasticity model for a thin, nonlinear, gradient elastic plate
   Int. J. Eng. Sci., 197 (2024), 104026, 17 pp.
6. Special Cosserat rods with rate-dependent evolving natural configurations
   (with K. R. Rajagopal)
   Int. J. Eng. Sci., 191 (2023), 103890, 19 pp.
7. On an elastic strain-limiting special Cosserat rod model
   (with K. R. Rajagopal)
   Math. Models Methods Appl. Sci., 33 (2023), p. 1-30.
8. On evolving natural curvature for an inextensible, unshearable, viscoelastic rod 
   (with K. R. Rajagopal)
   J. Elast. (2022), https://doi.org/10.1007/s10659-022-09956-7.
9. Global well-posedness for two dimensional flows of viscoelastic rate-type fluids
   with stress diffusion (with M. Bulícek, J. Málek)
   J. Math. Fluid Mech., 24 (2022), Paper No. 61, 19 pp.
10. Longitudinal shock waves in a class of semi-infinite stretch-limited elastic strings
    Math. Mech. Solids, 27 (2022), p. 474–490. 
11. Dynamics of bubbling wave maps with prescribed radiation (with J. Jendrej, A. Lawrie)
    Ann. Sci. de l’ENS., (4) 55 (2022), p. 1135-1198.
12. On stretch-limited elastic strings
    Proc. R. Soc. Lond. A (2021), 477: 20210181, 15 pp.
13. Local well-posedness in Sobolev spaces for first-order conformal causal relativistic
    viscous hydrodynamics (with F. Bemfica, M. Disconzi, Y. Shao)
    Commun. Pure Appl. Anal. 20 (2021), p. 2279-2290.
14. Threshold dynamics for corotational wave maps
    Analysis and PDE, 14 (2021), 2123-2161.
15. Conditional stable soliton resolution for a semi-linear Skyrme equation (with A. Lawrie)
    Ann. PDE (2019), Paper No. 15, 59 pp.
16. Soliton resolution for corotational wave maps on a wormhole
    Int. Math. Res. Not. IMRN, 15 (2019), p. 4603-4706.
17. Soliton resolution for equivariant wave maps on a wormhole
    Comm. Math. Phys. 359 (2018), p. 375-426.
18. Scattering for radial energy-subcritical wave equations in dimensions 4 and 5
    Comm. Partial Differential Equations, 42 (2017), p. 852-894.
19. Profiles for the radial focusing energy-critical wave equation in odd dimensions
    Adv. Differential Equ., 21 (2016), p. 505-570.
20. A partial data result for less regular conductivities in admissible geometries
    Inverse Probl. Imag., 10 (2016), p. 247-262.