Radio Imaging of our Moon
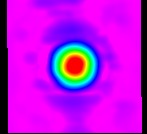
One of the most amazing things about modern technology is that it allows us to see the universe in many different wavelengths, not just optical ones. Believe it or not, this is actually an image of the moon, but taken in a different wavelength: radio. We can use this data after some processing for many things, but this blog will describe the process in which I used this radio data to determine the fluctuation of the Moon’s temperature throughout time.
This images was taken using the radio telescope at Green Bank in West Virginia. I used the L-band receiver, which takes in all wavelengths 1300 – 1800 MHz. I than narrowed down our spectral search to just 1355 – 1435 MHz to block out as much human-made radio interference. I then set the telescope to create a horizontal raster map, which creates the image above by sweeping the telescope side to side across the Moon to collect each pixel (radio telescopes have a 1 pixel camera). This observation was submitted by me to be taken on January 13. At the same time, my other lab-mates submitted 3 other images: one of the Moon on Jan. 15, of Virgo A (a star with a known flux density that we’ll use to calibrate the change in the Moon’s temperature) on Jan.13, and another of Virgo A on Jan. 15. Once all these observations came in, we were ready to calibrate the Moon’s flux density.
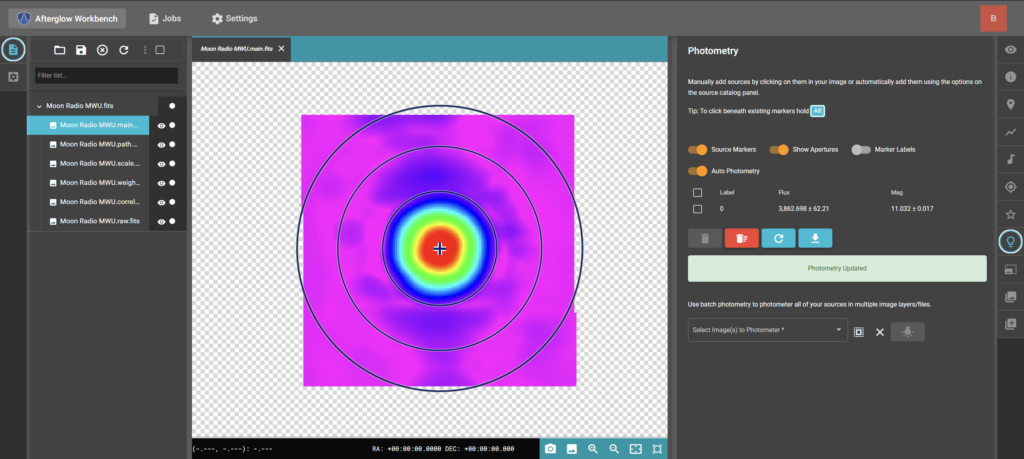
Firstly, we checked for any radio frequency interference — or “RFI” — in our observations. There was one small blip at the 1420 MHz mark, which is actually an emission line caused by cold hydrogen and not RFI. When processing our radio data to convert into a proper image, we can cut out any RFI we may have had along with other settings. These including removing the Earth’s own radio emissions from the image, and models to help gain more detail in the images (for example: to more clearly separate the Moon itself from its Airy rings, shown as the blue rings surrounding the radio Moon). After this, we are ready to bring the image into afterglow for processing.
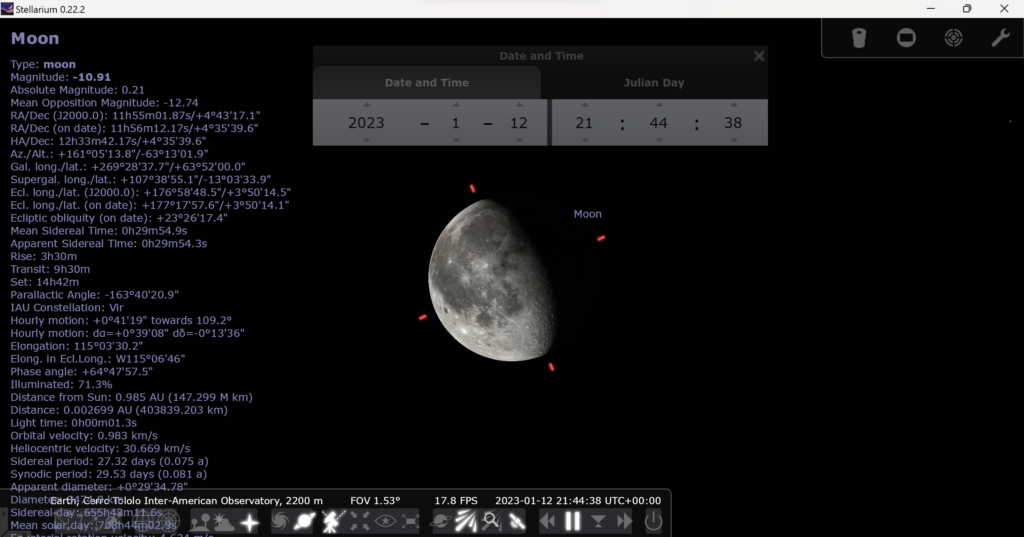
After tweaking a few settings for calibration to go smoothly, each member of the group used Afterglow’s photometric calibration operations to calculate their target’s flux from their image. Flux, however, is measured in an arbitrary unit. The reason we got data of Virgo A is so that we can get the Moon’s flux measurement in terms of Virgo A’s flux, which we did by dividing the Moon’s flux Virgo A’s. This measurement tells us how bright the Moon is in terms of Virgo A’s brightness at each respective date (Jan. 13 and Jan. 15). We then multiply the result by the known flux density of Virgo A (measured in Jy, or Janskys) to get us a real, usable measurement. Using Stellarium, a program that can give us various pieces of data about astronomical objects, we can also find the distance of the Moon from Earth at each respective date.
What is this all leading up to? Now that we have all the pieces, we can use the following equation to calculate the Moon’s average temperature, both inside and out!
S is flux density of the Moon in Jy, k is Boltzmann’s constant (1.38 × 10-23 J/K), c is the speed of light (3.00 × 108 m/s), v is the central frequency we measured at (1.395 × 109 Hz), d is the distance to the Moon from Earth in Km, and R is the radius of the moon (1737 Km). Here is our calculations throughout the entire process for the temperatures of the Moon:
| January 13: |
| Vir. A flux = 1,057.047 (calibrated from observation) |
| Vir. A known flux density = 229.2 Jy |
| Moon flux = 3862.689 (calibrated from observation) |
| Distance to Moon from Earth = 403046.501 Km (from Stellarium) |
| Moon flux density = (Moon flux) / (Vir. A flux) = 3862.689 / 1,057.047 = 3.654 Vir.A’s |
| Moon flux density = (Moon flux density) * (Vir.A flux density) = 3.654 Vir.A’s * 229.2 Jy = 837.5506 Jy |
| Moon flux density = 837.5506 Jy * 10-26 W/m2/Hz * 1 J/s = 837.5506 * 10-26 J/K |
| T = ( (837.5506 * 10-26) / 2(1.38 × 10-23) ) * (3.00 × 108 / 1.395 × 108)2 * ( (403046.501)2 / π(1737)2) ) |
| T = 240.5231412 Kelvin (-32.6268588 degrees Celcius) on January 13 |
| January 15: |
| Vir. A flux = 1,057.745 (calibrated from observation) |
| Vir. A known flux density = 229.2 Jy |
| Moon flux = 4601.191 (calibrated from observation) |
| Distance to Moon from Earth = 369608.606 Km (from Stellarium) |
| Moon flux density = (Moon flux) / (Vir. A flux) = 4601.191 / 1,057.745 = 4.35 Vir.A’s |
| Moon flux density = (Moon flux density) * (Vir.A flux density) = 4.35 Vir.A’s * 229.2 Jy = 997.02 Jy |
| Moon flux density = 997.02 Jy * 10-26 W/m2/Hz * 1 J/s = 997.02 Jy * 10-26 J/K |
| T = ( (997.02 Jy * 10-26) / 2(1.38 × 10-23) ) * (3.00 × 108 / 1.395 × 108)2 * ( (369608.606)2 / π(1737)2) ) |
| T = 240.7817756 Kelvin (-32.3682244 degrees Celcius) on January 15 |
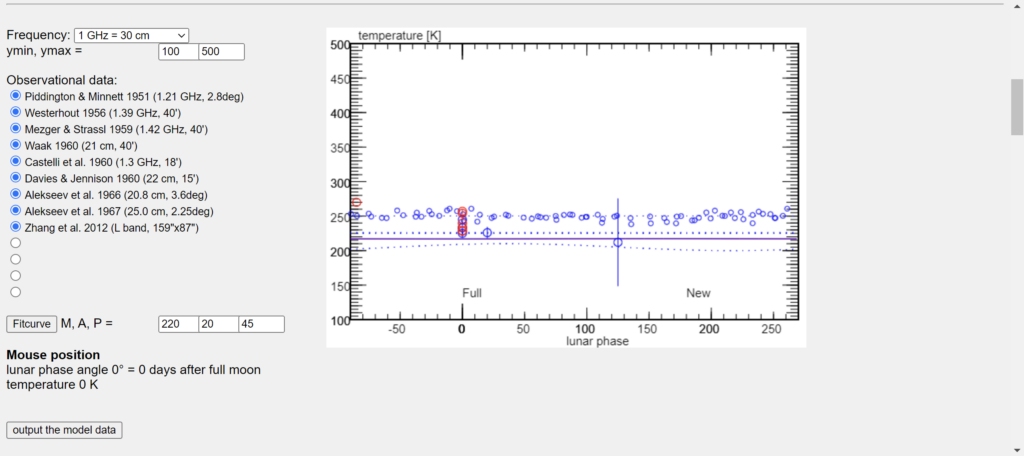
So what does this all mean? What we measured was actually the Moon’s internal temperature. If there was a significant difference between the temperatures on our 2 dates of measurement, then we could account this difference to the changes of the Moon’s phase (61.1% full on Jan. 13 and 20.6% full on Jan. 17). However, since we don’t see any significant change in our data, then we can safely say that our temperature measurement is that of the entire Moon inside and out, not just it’s illuminated surface! We also had the opportunity to see how our data compared to that collected by professional astronomers (pictured below). You can see how our data falls neatly inside the range of temperatures collected by the pros. This means that our data is not only scientifically accurate, but scientifically awesome as well!