Invisible Brightness
Observing the Moon in Radio Wavelengths

In the previous post, we observed the moon through visible light. Since the moon reflects the sun’s light, its visual brightness fluctuates with the change in phase. In this post, we wanted to see if these changes in brightness hold true across different wavelengths of the electromagnetic spectrum, specifically radio waves. Radio waves have the longest wavelengths and lowest energies in the spectrum, which means they would be the least likely to correspond with light from the sun, which is mostly visible, infrared, and ultraviolet.
The Process
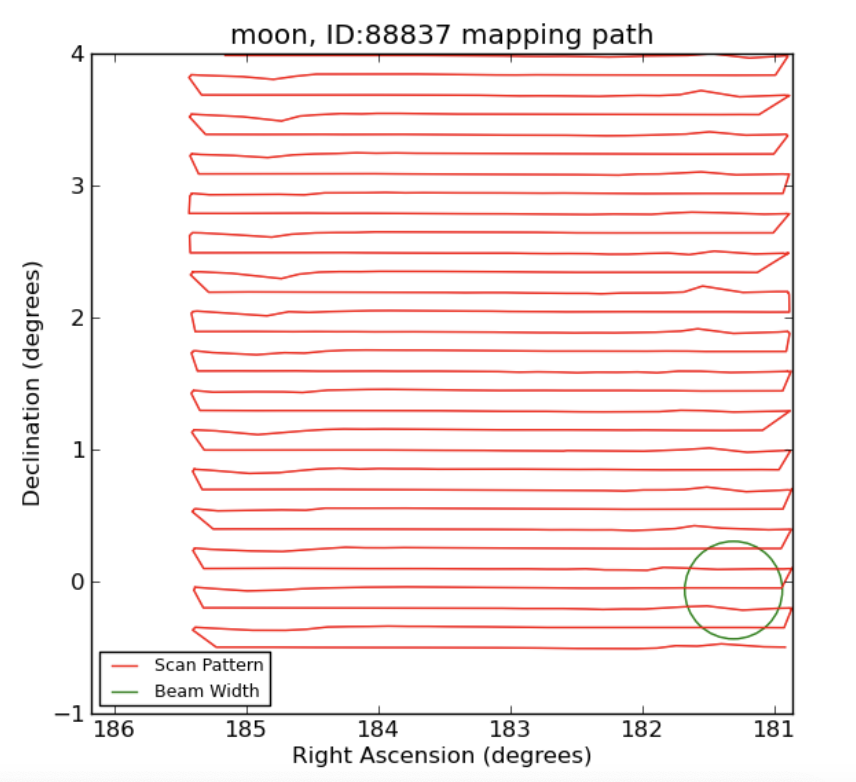
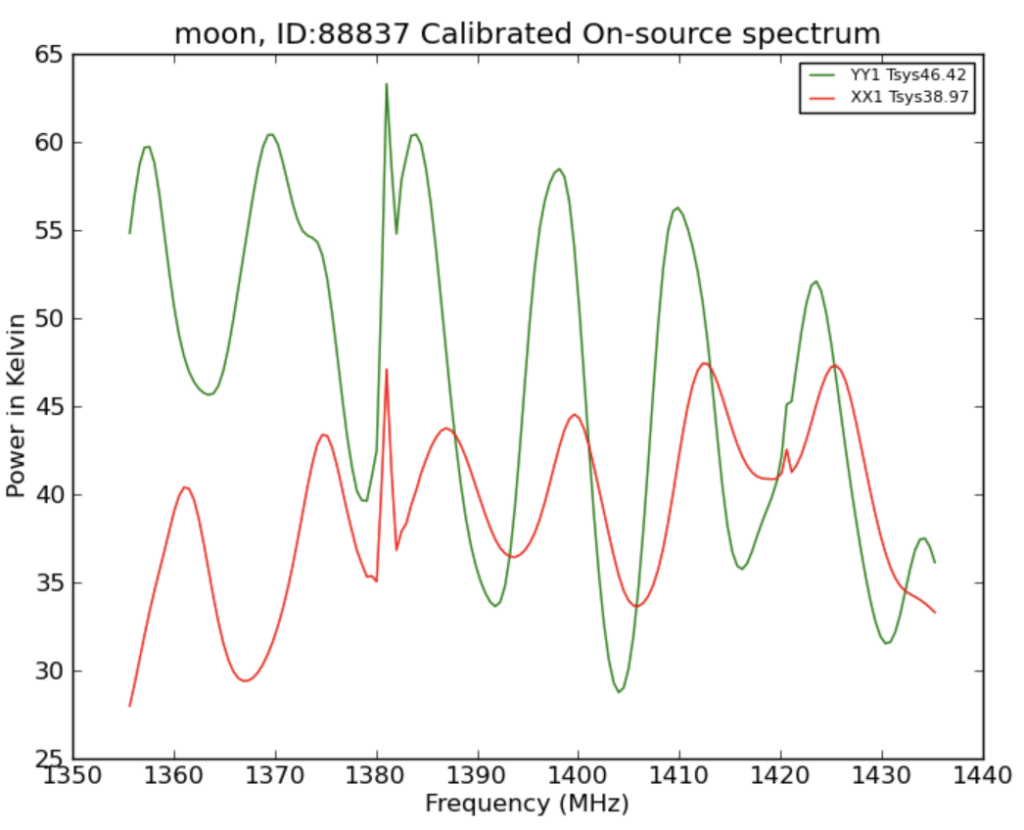
In order to calculate potential changes in brightness, we had to take radio images of the moon during different phases, as well as another object that could serve as a standard for comparison. Our group took images of the moon and the galaxy Virgo A on 2 separate days, one where the moon was a waning gibbous and one where it was a waning crescent. We used the 20m radio telescope at the Green Bank Observatory in West Virginia. The telescope used a raster pattern (shown below) to create the image. From our results, we filtered out the wavelength of 1381 nm, since this was a wavelength used in manmade transmissions (as seen in the spike below). We were then able to use aperture photometry in Afterglow in order to receive a flux density value for each image (the current moon, current Virgo A, delayed moon, and delayed Virgo A).

The Calculations
In order to compare the radio brightness of the two moon phases, we had to convert them to a ratio against the brightness of Virgo A. We found that the waning gibbous phase (at 66% of a full moon) had a flux density (comparative value of radio wave emission) of 878.74 janskys (Jy) and the waning crescent phase (at 25% of a full moon) had a flux density of 921.76 Jy. This shows that more radio waves from the moon reached Earth at the waning crescent phase than the waning gibbous phase. As a result, radio wave emission from the moon is not dependent on the light from the sun. Instead, it is a more constant value that comes from the moon’s natural internal radiation.
All objects in the universe emit some wavelength of light. For example, the sun emits mostly visible, infrared, and ultraviolet light, while the Earth emits mostly infrared light. This is due to the temperature of the object. Hotter objects like stars emit shorter frequencies of light, while cooler objects like planets emit longer frequencies. Since we know that the moon is emitting light in radio waves, and we know the flux density value in Jy, we can use the formula below to estimate the internal temperature of the moon.
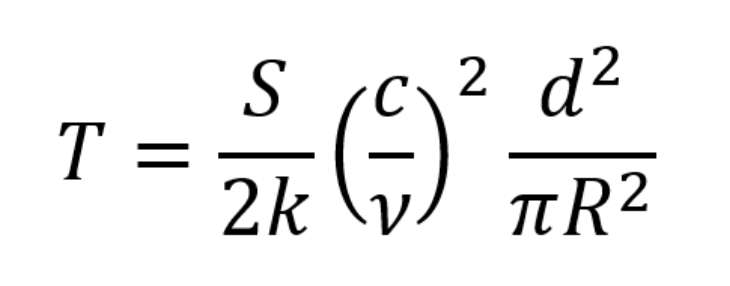
Using this formula and the flux density of the moon measured at the two phases, we estimate the temperature of the moon to be around 222.41 – 240.59 Kelvin. This is approximately -59.33 to -26.61 degrees Fahrenheit. For comparison, winter temperatures in non-coastal parts of Alaska typically fall to -30 degrees Fahrenheit. According to NASA, the moon’s true blackbody temperature is 270.4 Kelvin, which is not too far from the temperatures we calculated.
While we can not see radio waves, observations using them can actually tell us a lot about the worlds beyond our planet. We know that emissions in the radio spectrum do not always correspond to the other forms of radiation, and that measuring specific wavelengths of emissions can help us find the inner temperatures of other objects in space. As we use our telescopes to journey deeper into the Solar System and beyond, we will continue to observe how light and color affect the way we see the universe.