The Birth of Stars
Using Multi-Wavelength Photography to Understand Star-Forming Regions
By: Nat Heddaeus, James Thompson, Rujula Yete
Observation Details
We observed the star-forming region (SFR) IC 2944, also known as the Running Chicken Nebula. Observations were made using the PROMPT-5 Telescope, stationed at Cerro Tololo Inter-American Observatory, Chile. We used the visible light filters R,V,B and Lum (Red, Green, Blue, and Luminance; observation credit to Rujula Yete), with observing times of 100, 150, 200, and 90 seconds respectively, and the narrowband filters Halpha and OIII (observation credit to James Thompson), with 600 second observing times for both filters.
Image Processing
Once our images came back, per usual they were cleaned, aligned, and stacked by their respective filters. For our star forming region, we used R,B,V, and Luminance filters, Halpha and OIII narrowband filters, and some supplemental infrared filters which we will discuss later.
The first step towards creating our images was to assign colors to our layers. R,B, and V were assigned red, green, and blue respectively with the screen blend mode. Luminance was left as gray, but assigned the blend mode luminosity. Narrowbands Halpha and OIII were assigned blend mode lighten, with the color maps balmer and OIII. The colors of the narrowbands were later changed for aesthetic purposes. All layers were synced to luminance and color calibrated using WCS, and an extinction value (E(B-V) or reddening) of 0.320. Using the luminance layer, midtone level was adjusted to taste. Narrowbands were then desynced, and adjusted.
The narrowband filters supplied additional color to our images, allowing us to see some of the physical processes at play in the Running Chicken. Halpha allows us to see the hydrogen gas floating around in the star forming region. Hydrogen is the most abundant element in the universe. Note how dominant pink our star forming region appears before the addition of WISE and Spitzer data. That pink is our hydrogen, which is using the balmer color map.
Also note the subtle blues floating around, our OIII. In the image below, OIII uses the harmony color map. OIII is twice-ionized oxygen, which emits in the blue-green part of the visible light spectrum. Note how it resides around our image’s brightest stars. The pinks and blues of our images give us insight into the processes of play in our star forming region. We will go more into depth in the next section, but for now, know that their colors are also a sign of the area’s temperature. Hydrogen has temperatures of at least 5000K, and OIII of at least 15,000K.

The midtone of the Halpha and OIII stacks were separately to bring out the natural color of the gasses in our image. Due to the lighten blend mode, stellar colors remained as was, while Halpha and OIII could be adjusted to add just enough color to the region. After this step, slight tweaking was done to reduce the noise of our images, and the narrowband color maps were changed by aesthetic preference.
Our images were still lacking in detail, which led to us adding images taken in the infrared to supply our images with more depth. The first infrared layer we added was 2MASS, or the 2-Micron All Sky Survey data. This allowed us to see background stars that we cannot see in the visible light spectrum and that warm the regions around them. The 2MASS data was given the cool color map and lighten blend mode.

To add even more depth to our images, we added archival infrared data from WISE-12, WISE-22, and Spitzer (varies depending on image). For the image below, we used WISE-12 data with the heat color map and blend mode screen, and IRAC-4 Spitzer data with the cool color map and blend mode screen. The addition of infrared data to our image allows for us to see more of the warmer dust that doesn’t appear in the visible part of the spectrum.

The Physical Story
Stars form from dust and gas. When large amounts of these materials condense, gravity can cause them to collapse in on each other, forming heat-producing cores that eventually become stars. As a result, star forming regions are full of dust, gas, and stars.
In the bottom right corner of our images, we can see two bright blue stars. Stars like these are extremely hot and bright, with possible temperatures ranging from 10,000 to 50,000 Kelvin. The stars are also very young. Stars in star-forming regions, such as the Running Chicken Nebula, are in their earliest stages of life, with large amounts of fuel burning at high rates to emit massive amounts of energy in the form of light. While radiation is produced across the electromagnetic spectrum, a significant portion of light produced by younger stars is ultraviolet light. This high energy wavelength excites electrons in the atoms it interacts with. In star-forming regions, it typically interacts with gas atoms. After the light passes, the excited electrons return to their previous states, emitting the energy at various discrete wavelengths. In the Running Chicken images, we can see this emission as the colorful regions captured by the narrowband telescope filters. The most prominent emission line, Halpha, is a red color at the 656 nanometer wavelength, produced by emission from the hydrogen atom. When mapped to the Balmer color map, we can see this in shades of pink, which is the most prominent in our image. Halpha emission occurs between 5,000 and 10,000 K. This indicates that hydrogen is very abundant in this nebula, and that majority of the region is in the Halpha emission temperature range. We also collected images from the OIII narrowband emission. This emission line is a blue-green color at around 500 nm, produced by emission from doubly ionized oxygen atoms. While not directly visible in our images due to the strong presence of hydrogen, areas with more ionized oxygen appear cooler (in color) and less pink, especially near the two bright stars. This is mostly because the energy required to excite the oxygen atoms is more than the energy needed to excite hydrogen atoms. OIII emission occurs between 15,000 and 40,000 K. More UV radiation energy is present closer to the stars, so more OIII emission can be found there.
While the visible wavelengths paint a picture of the stars and gas, invisible wavelengths can tell us more about dust. Similar to gas, ultraviolet light from stars also interacts with dust. However, the light causes dust to heat up, emitting radiation in the infrared wavelengths. For our images, we used archival data to incorporate infrared emission. The WISE-12 data (shown with the heat color map) shows emission detected from dust heated to 300 K. This is seen closest to the prominent stars, as well as in areas farther from the large area of hydrogen gas, indicating that these are warmer regions of the nebula. The Spitzer data (shown with the cool color map) shows emission detected from dust heated to 100 K. This is not as obviously seen in the image, but is present near the edges of the hydrogen areas, indicating cooler regions. The 2MASS data shows stars that have been detected through infrared radiation. These stars are usually not visible through optical observing because their visible light is blocked by dust. In the central lower area of the optical image, we can see a dense pink cluster of hydrogen with a bright star seemingly in the middle. Through the 2MASS data, we can see 2 stars in that location, implying that the stars are behind the gas and some layer of dust.


Comparing our images to an image of the Running Chicken from the European Southern Observatory shows a very similar story. The area near the stars is less pink, likely due to the presence of hotter gas. The large patch of hydrogen dominates the center, while on the other side dark red shows areas of hot dust. As energy from existing stars interacts with dust and gas, it causes particles to heat up and move around. This could lead to concentrations of dust and gas that, if dense enough, could produce even more stars. As a result, all of the processes taking place in a star-forming region drive each other. By observing the Running Chicken Nebula through a variety of wavelengths, we can see the effects of these processes taking place. While these results may seem expansive, they only cover the tip of the iceberg. Other wavelengths, such as X-ray and radio (which we were not able to obtain in the Southern Hemisphere), can provide even more information about the star forming life cycle. Observing through multi-wavelength tools helps us visualize the formation of our universe, as well as perform calculations to gain a precise understanding of what we can see.
Calculations
As discussed above, the bright blue stars driving this region emit ultraviolet-frequency photons that ionize the surrounding gas; that is, they separate the electrons and protons making up the hydrogen atoms nearby (the gas mostly consists of hydrogen; for simplicity we ignore anything else present). This process is counterbalanced by another process, the occasional recombination of protons and electrons into hydrogen atoms. As a simplified model, we suppose that the star is surrounded by a sphere within which hydrogen is ionized, and that outside the sphere hydrogen is not ionized (and, because it isn’t hot, it exists as H2 rather than free hydrogen atoms). In order for this situation to be stable, the amount of ionization that occurs within the sphere has to be just enough to counteract the recombination that occurs inside. Mathematically, this ends up coming out as follows:
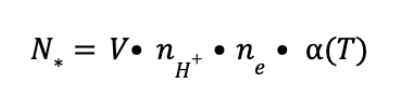
where N* is the rate at which the star emits photons, V is the volume of the sphere, nH+ is the number density of hydrogen ions (i.e., a value giving the number of hydrogen ions in a given volume), ne the number density of electrons, and (T) is value representing the chance of recombination that can be computed from subatomic physics and which dependes on the temperature of the region.
Now, since all of the hydrogen ions and electrons are coming from hydrogen atoms breaking up, their densities should be equal nH+=ne. Using this fact and substituting in the expression for the volume of a sphere and a value for (T) based on existing estimates of the temperature of star-forming regions, when we solve for nH+, we find the following:
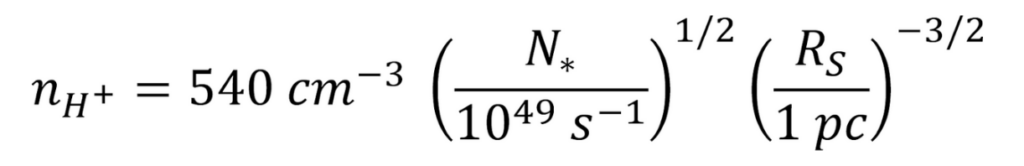
where RS is the radius of the sphere. Thus, all we need to do to estimate the density of hydrogen is to obtain values for N* and Rs. To get a value for Rs, we first measured the angular radius of our region in the free observatory program Stellarium:

We can use this angular radius in combination with the distance of our region to determine its actual radius using basic trigonometry. Fortunately, its distance was already obtained by the Gaia spacecraft which measured it to be 6523 lightyears, or 2000 parsecs. This gives a radius of 10.1 parsecs for the region.
To determine N*, we need data on the intensities of the stars in our region. Rather than scouring the literature ourselves, we got a little (authorized) help from ChatGPT, which informed us that the brightest stars in this region are HD101131 and HD 101205. Based on known information about these stars and about how many photons stars of different sizes and temperatures emit, we can estimate the total ionizing flux for this region to be 7 * 10^47 photons / second. Plugging in these values, we get a density of 4.45 ions per cubic centimer. This is somewhat lower than is typical for these regions.
Next up, we use this number to estimate the number density of H2 outside the sphere. It turns out to be harder to estimate directly; we can just get a lower and upper bound. These come from two particularly simple states the region is in at different times: first off, when the star first forms, all of the gas being ionized in the sphere was formed by just breaking up H2, with no expansion or contraction, so the density inside the sphere should be twice as much as the density outside. This gives us an estimate for the outside density of 2.23 molecules of H2 per cubic centimeter.
However, over time, the ionized region expands, making the density inside lower, which implies that the value above for the outer density is just a lower bound. However, eventually the sphere should end up in pressure equilibrium: the pressure due to the protons and electrons inside should equal the pressure due to the H2 on the outside. As this point, using the ideal gas law, we must have the following relationship:
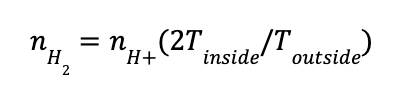
where Tinside is the temperature inside the sphere and Toutside the temperature outside.
Thus we just need to estimate the temperature inside and outside. For this, we can look back at our image: we see H-alpha narrow-band emission near the edge of the region, which implies a temperature of the gas of about ~5000 K – 10000K. Outside, we see thermal emissions from the dust of wavelength roughly 12 microns. A result called Wien’s Law gives a relationship between wavelength of thermal emissions and temperature: the wavelength we observe implies a temperature of about 242 K. (we assume the gas and dust outside are the same temperature.) Hence we end up with a density estimate of 180 molecules of H2 per cubic centimeter.