(The above image is stylized for effect, please see the image below for their unaltered version.)
This article was composed in partner with Andreas Buzan, Alyssa Manus, and Ruby McGhee. Please see the credits for more information.
About the Image
Overview
For this module, we began with optically observing the star-forming region (SFR) Messier 78. We used PROMPT 6 for our filters B, V, R, and Lum. For our narrowband filters (OIII and Halpha), we used PROMPT 7. Our total observing time per filter is as follows: B= 1090.0s, V= 350.0s, R= 240.0s, Lum= 270.0s, OIII= 1500.0s, and Halpha= 1500.0s. The luminance filter allows us to boost the signal-to-noise ratio of our image. The narrowband filters allow us to bring out the gas content in our image. Our final image is a compilation of our initial observations and archival mid-infrared (MIR) and near-infrared (NIR) data. The archival data helps reveal stars hidden by dust at the NIR wavelengths and dust that is heated by stars at the MIR wavelengths.
RGB Images
After collecting images, we noticed a combination of ghosts (bright images whose light wasn’t entirely removed before taking our images) and smears across some of the RGB images. We attempted to retake these images many times over, but in order to budget the group’s credits to collect other data, we chose enough images from a series of other observations made by Dr. Dan Reichart to combine with our own data to remove the contaminated areas from our final image. We loaded these images along with our own into Afterglow, and aligned them all to one single image to frame them all correctly. After then using a pixel operation to clean up the data, we took each image of each filter and used the stacking tool with Chauvenet rejection as well as SNR smart stacking to try and remove the contaminated areas as much as possible. Even though this didn’t remove it entirely, we were also able to use the Lum data (of which there was a lot more without contamination) to erase the little contamination remaining. We took the RGB stacks and using the new Afterglow system, linked them to the Lum stack with luminosity blend mode, and used the photometric color calibration settings to balance the RGB stacks to their true values, creating a great optical image of M78. The E(B-V) reddening of this nebula wasn’t known, so we used an estimated value of 0.5, as M78 is a reflection nebula, and so would have a large amount of dust between it and Earth by default since it’s using that dust to reflect its light towards us. After that, we simply adjusted the background and midtone levels of the Lum layer to reveal as much depth in the nebula as possible.

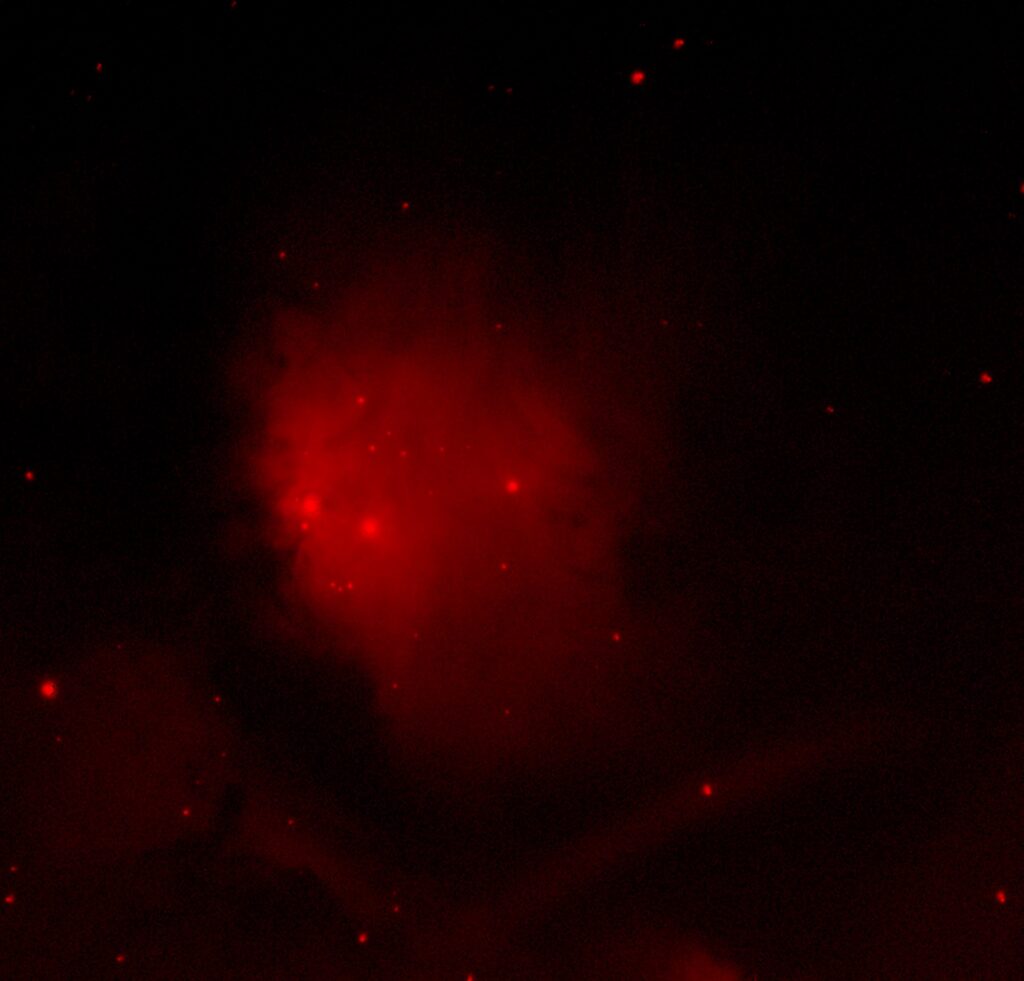
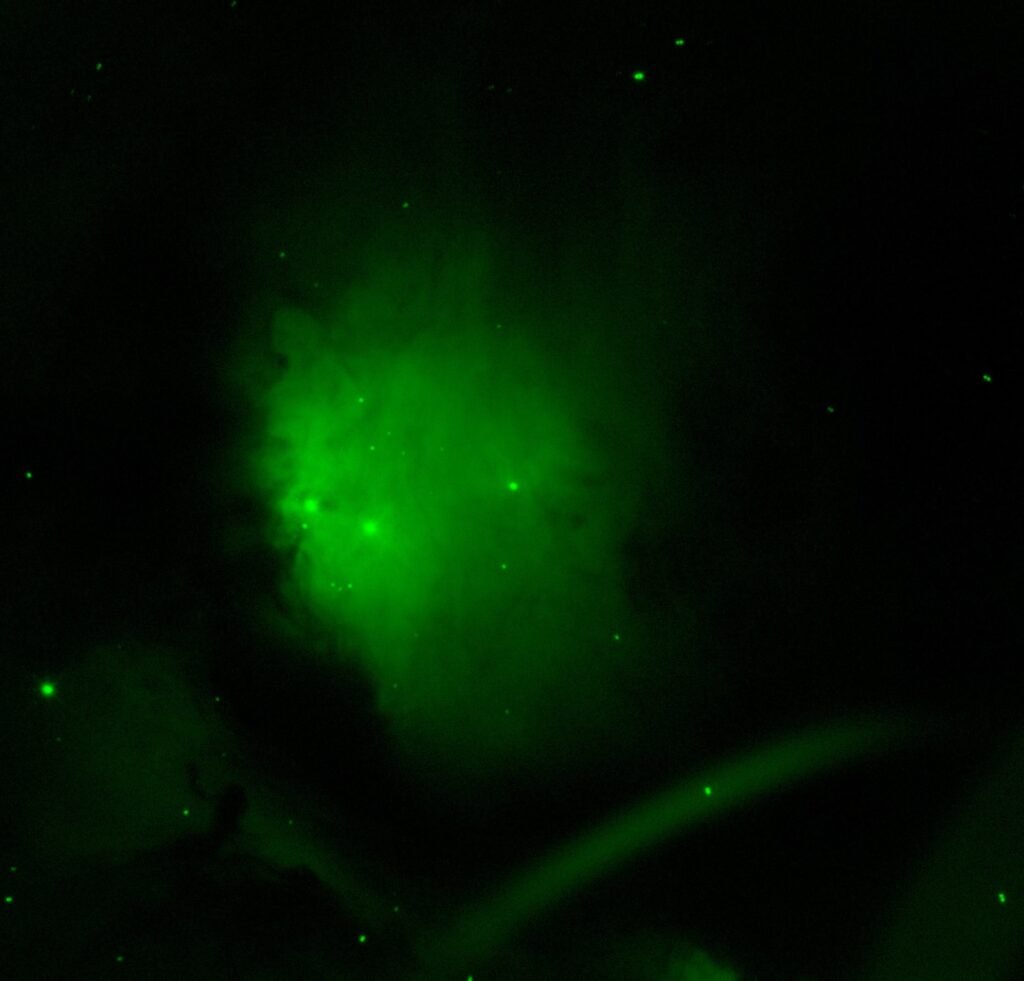
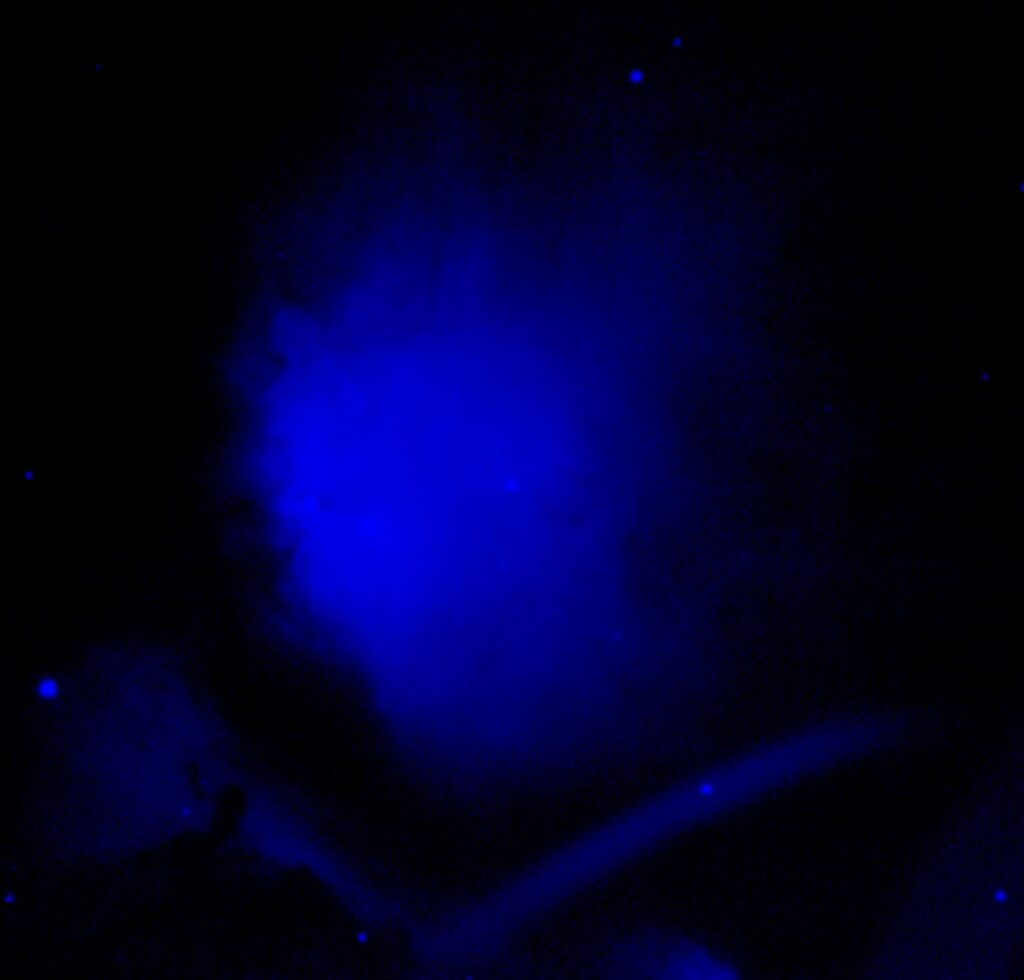
Narrowband Images
We waited for the Moon’s bright cycle in order to use Prompt 7’s 600 second exposures to use, as the Moon’s light wouldn’t interfere as much with narrowband (NB) as with RGB images. Sadly though, the images that returned came back so dim, grainy, and without detail that they were nearly unusable. We tried making the best of them regardless and after aligning, cropping, coloring (Balmer for Halpha and OIII color for OIII), and stacking them like the RGB images, we used every trick in the book to bring them out as much as possible. Instead of setting the NB to lighten blend mode, we set them to screen, and put them underneath the Lum layer to make them controlled by the Lum to reduce noise. The data was so bad in these images that even with all this, we still had to change the background and midtone levels to dim them down to nearly nothing to keep them from making the whole image grainy. I think the reason they came out so bad was because the dust causing the reflection of the nebula was interfering with the narrowband more than with the optical data.


NIR and MIR Images
The final step was to import data from various space telescopes to add thermal data to our images. We went to the Skyview Virtual Observatory and entered our specific coordinates that we centered on to get our image into the database. Tweaking a few more settings let us get images in the same quality size as our RGB/NB images. We downloaded MIR data this way from WISE 12, WISE 22, and 2MASS-K to collect 300K, 100K, and dust-hidden star data respectively. We then went to the Spitzer Data Archive to get data from the IRAC 4 telescope, providing us with more data similar to WISE 12 (WISE 12 measures at 12 microns while IRAC 1 measures at 8 microns). Importing them into Afterglow, we aligned, cropped, and colored the datasets to fit them into our image. There was a small tear in the IRAC 4 data from oversaturation, so we used the “img.filled(img.max())” command to fill that gap with the max pixel value possible (white) before aligning and cropping. This also added a lot of white on the edges of the image, but since it was then cropped it was all removed in the final image. We used the heat color palette to color IRAC 4 and WISE 12 to show hot gas, cool color palette for WISE 22 to show cold gas, and blue-green color palette for 2MASS-K so the background stars show easily. The blend modes for all these datasets are all screen, except for WISE 22, which we set to lighten to keep the blues of the nebula and blues of the cold gas distinct. The final step was to adjust background, midtone, and saturation levels to bring out the best quality of the images so they all appeared bright and easy to analyze in the final image.
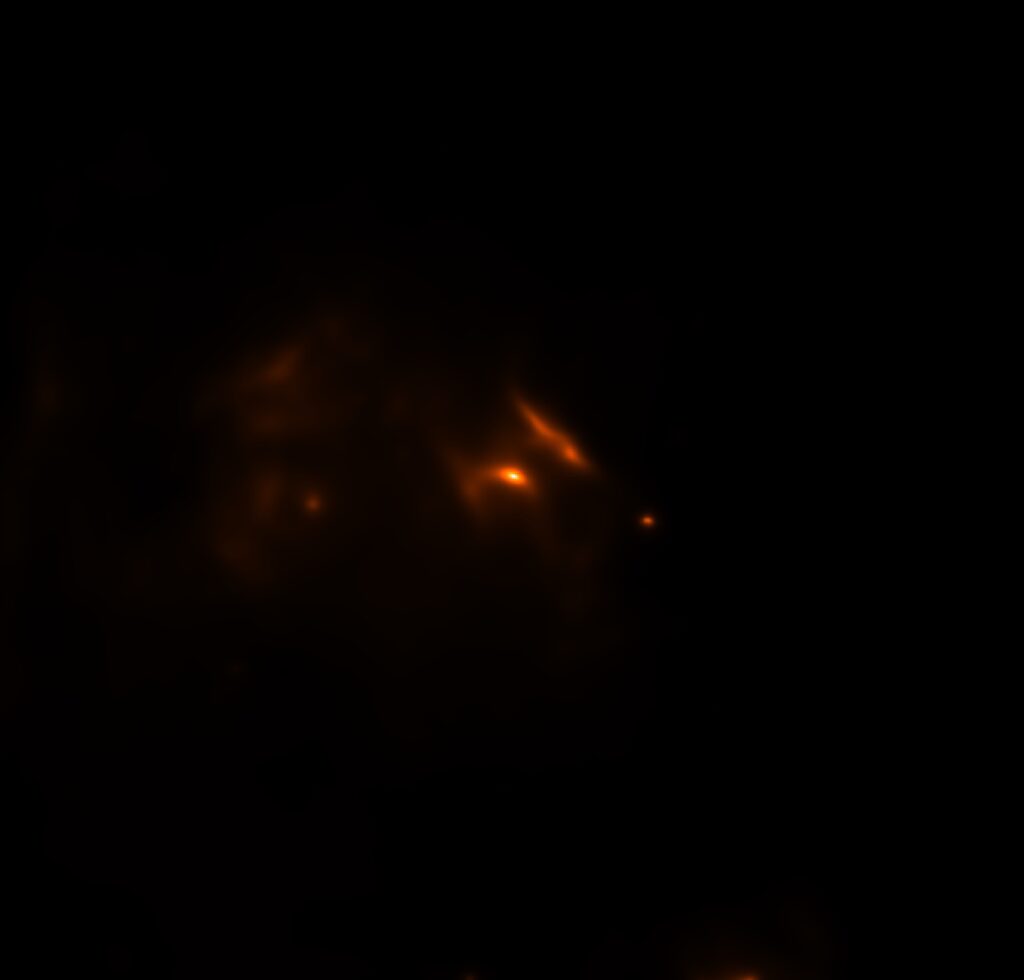




The Physics
Physical Processes
Messier 78 is classified as a reflection nebula because it has a small amount of ionized gas and reflects the light of the stars around it. These bright, hot, blue stars emit light at UV wavelengths which excites and ionizes the gas surrounding them. Our filters Halpha and OIII are the narrowband emission lines produced from the de-excitation of the gas and are regions known as emission nebulae. The bremsstrahlung radiation in our image is detected at the radio wavelengths and was created from the ionization of the ions (mainly protons) that interacted with the free roaming electrons in the hot dense gas of M78.
Our MIR archival data comes into play from the UV radiation that heats the surrounding dust which is immersed in the gas and then re-emits the energy as thermal or blackbody radiation at longer MIR wavelengths. Using our NIR archival data, we can use near-infrared wavelengths to spot the stars hidden in the dark nebulae regions where no stars can be seen at optical wavelengths. Dark nebulae regions are the densest portions of the dust that scatters optical light and reddens the stars behind it.
Reflection nebulae on the other hand, is a result of the dust scattering optical light making entire regions visible and appearing brighter and bluer. Star formation occurs when non-transparent clumps made of gas and cold dust reach their minimum threshold of mass needed for the chain of events for the birth of a star to begin and results in the collapse of these clumps under their own gravity. Later in the life of the star forming region, the cold gas pushes up against the hot expanding gas creating dense clumps of pillars, columns and spires. Then these structures are squeezed to create globules that eventually collapse and contribute to the formation of the next generation of stars in our nebula. This cycle of stellar life is cyclic and continues until our universe runs out of usable energy but, by then, humans should be a faint cosmic blip of the past in the grand scheme of the universe, so there is no need to worry!
Density Calculations
Context
It’s not a surprising thing to say that the largest stars emit tons of radiation in the form of photons, and particularly high-energy photons can transfer so much energy to an electron that it can overcome the electromagnetic force attracting it to the nucleus and knock the electron free. This leaves the atom with an imbalance of charges, which makes it an ion; ions can eventually regain a balance of charges if an available electron is found and recaptured.
Hydrogen is the most abundant element in the universe as a pair of one electron and one proton, and ionizing radiation is able to turn a hydrogen atom into a free proton and electron. Within many star-forming regions, there exists an area in which hydrogen gas near the brightest stars is being ionized much more quickly than it can recombine: this area is called the HII region, where H is the chemical symbol for hydrogen and the roman numeral II denotes that the atom is singularly ionized (HI would denote that the hydrogen atom is neutrally charged). This region is contained in the Strömgren sphere, an imaginary divider between the internal HII region and external HI region that is defined as being the point at which the rate that hydrogen atoms being ionized is equal to the rate at which the resulting protons and electrons are recombining.
Internal Density
To estimate the radius of the Strömgren sphere in parsecs, determine the distance from the brightest stars in the nebula to the edges of the nebula in degrees and then multiply that value by the distance to the nebula in parsecs. For M78, the brightest stars were estimated to be about two-thirds of a degree from the edge of the nebula, and being that M78 is around 490.6 parsecs away, the radius of the Strömgren sphere would be about 5.7 parsecs.
From here we can estimate the number of protons (ionized hydrogen) in the HII region, but we must first know the amount of ionizing radiation the brightest stars are emitting. This amount, the ionizing flux, is related to the star’s spectral class, a classification of the different temperatures of stars: the hottest stars are of O or B class, and classes are internally ranked from 0 to 9.9, 0 with being the hottest ranking in the class. In M78, we gather that there are two B2 stars, and B2 stars maintain approximately 6 × 1044 Hz of ionizing flux. Since there are two B2 stars, there is 1.2 × 1045 Hz of ionizing flux driving the HII region. Now, we can calculate the density of hydrogen in the HII region: to do so we must multiply 540 by the root of the amount of ionizing flux divided by 1049 and multiply all of that by the inverse of the cube of the root of the Strömgren radius (got all of that?). Doing so, we estimate that the density is 0.4 hydrogen atoms per cubic centimeter.
External Density
But what about the density outside of the HII region? Well, that is a much more involved calculation, but we can at least determine upper and lower bounds for the density. The region around the stars was likely very cold before the stars ignited, and this region was likely filled with an abundance of H2, a molecule consisting of two protons and two electrons (helium has an additional two neutrons, in case you were wondering). The ignition of the stars would split the dihydrogen into two H+ (HII) atoms, and as the radiation of the star is continually emitted, the Ströngren sphere would expand with the H2 being split apart. As a lower limit, we can assume that all hydrogen in the nebula outside of the Strömgren sphere exists as dihydrogen, and as such the density would be equal to the density of the HII in the inner region divided by 2. Doing so sets the lower limit of the density of the regional 0.2 atoms per cubic centimeter.
Finding the upper limit is a much more involved process: the HII region expands due to heat, and it would be incredibly difficult to determine just how much it has expanded without knowing how old the stars were. However, the region cannot expand infinitely: its limit is when the pressure inside the Strömgren sphere is equal to the pressure outside of the sphere. Chemistry tells us that the pressure of an ideal gas is a function of the density of the gas multiplied by its temperature all multiplied by Boltzmann’s constant; since we are setting up a proportion, we can disregard the constant. To determine the temperature of the inner region, one would usually estimate by the amount of emission detected by the narrowband filters, but the data we collected was not suitable for this purpose. We deduced that the inner temperature was below 5000 kelvins (K), and so approximated 3000K as a suitable inner temperature. For the outside region, we looked to the emissions in our MIR data and found that our WISE12 data on the edge of the nebula would be suitable for temperature derivation: to do this we used Wein’s law, where the peak of the thermal spectra is equal to 2900K divided by the wavelength of the emissions in microns. WISE12 detects emissions at 12 microns, so the temperature at the edge of the nebula was estimated to be 240K (about -33°C, -28°F). Solving the proportion by multiplying the density of the inner region by the temperature of the inner region divided by the temperature of the outer region, it is revealed that the upper limit of the density of the outer region is some value around 5 atoms per cubic centimeter.
Credits
Thank you to Andreas Buzan for allowing me to feature and edit his image of M78, and for writing the sections on how the data was collected and the physical processes at play. Andreas maintains his own blog at tarheels.live/blogandreas/.
As well, thank you to Alyssa Manus for writing the sections on how the radio spectrum data was collected and the physical processes at play. She also runs her own blog at alyssacmanus.wixsite.com/astrophotography.
And as well, thank you to Ruby McGhee for writing the overview of how the data was collected and the section on the physical processes at play. Her blog can be found at tarheels.live/rubymcghee/.
And finally, thank you to Dr. Dan Reichart for providing supplementary data for the image. He also runs his own Afterglow astrophotography blog at www.danreichart.com/afterglow-astrophotography.
Proudly powered by WordPress
